[데이터 시각화] 2. 분포 시각화
by Rev_> data <- read.csv("C:/BNG/diamonds.csv", header=T) # data를 불러 옴
> str(data) # str : 데이터에 대한 구조 또는 변수 정보
'data.frame': 53940 obs. of 11 variables:
$ X : int 1 2 3 4 5 6 7 8 9 10 ...
$ carat : num 0.23 0.21 0.23 0.29 0.31 0.24 0.24 0.26 0.22 0.23 ...
$ cut : chr "Ideal" "Premium" "Good" "Premium" ...
$ color : chr "E" "E" "E" "I" ...
$ clarity: chr "SI2" "SI1" "VS1" "VS2" ...
$ depth : num 61.5 59.8 56.9 62.4 63.3 62.8 62.3 61.9 65.1 59.4 ...
$ table : num 55 61 65 58 58 57 57 55 61 61 ...
$ price : int 326 326 327 334 335 336 336 337 337 338 ...
$ x : num 3.95 3.89 4.05 4.2 4.34 3.94 3.95 4.07 3.87 4 ...
$ y : num 3.98 3.84 4.07 4.23 4.35 3.96 3.98 4.11 3.78 4.05 ...
$ z : num 2.43 2.31 2.31 2.63 2.75 2.48 2.47 2.53 2.49 2.39 ...실습을 위하여 위와 같은 53940 X 11 데이터를 불러왔다.
빈도 분석
빈도 분석은 범주형 변수에 대해서만 분석한다.
> table(data$cut) # table() : 빈도분석 수행
Fair Good Ideal Premium Very Good
1610 4906 21551 13791 12082
> table(data$color)
D E F G H I J
6775 9797 9542 11292 8304 5422 2808
> table(data$clarity)
I1 IF SI1 SI2 VS1 VS2 VVS1 VVS2
741 1790 13065 9194 8171 12258 3655 5066table() 함수를 이용하여 빈도 분석을 수행할 수 있다.
해당 변수에서 각각의 데이터가 몇 개씩 있는지 알 수 있다.
table(data$cut)을 예를 들어 본다면 cut 변수에서 Fair 데이터가 1610개, Good 데이터가 4906개, Ideal 데이터가 21551개, Premium 데이터가 13791개, Very Good 데이터가 12082개 있다는 의미이다.
막대 그래프
barplot(table(data$cut), xlab="cutting status", ylab="frequency", main="barplot for cut")barplot() 함수를 사용하여 막대 그래프를 그릴 수 있다.
xlab = "" 은 X-축 제목, ylab = "" 은 y축 제목, main은 그래프 전체 제목을 의미한다.
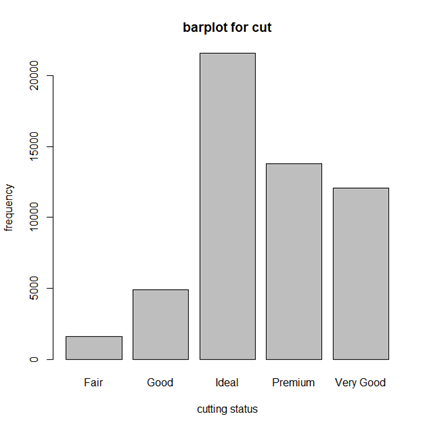
다이아몬드 커팅 상대에 대한 빈도 분석 결과를 살펴보면,
Ideal이 가장 많은 빈도를 차지하고 있고, 그 다음으로 Premium, Very Good, Good, Fair의 순서이다.
원 도표
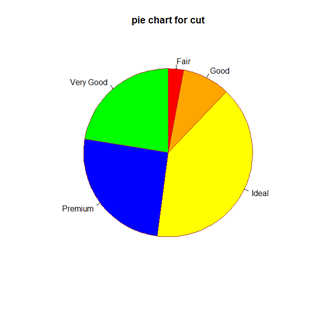
pie(table(data$cut), main="pie chart for cut",
col=c("red", "orange", "yellow", "blue", "green"), border="brown", clockwise=TRUE)pie() 함수를 사용하여 원 도표를 그릴 수 있다.
col을 통하여 각각의 색깔을 지정할 수 있다. col 옵션을 col=gray(seq(0.2, 0.8, length=5)와 같이 설정하면 회색 계열을 0.2에서 0.8까지 5개의 톤으로 나누어서 색을 지정하게 된다.
border 옵션은 파이 조각의 경계선 색상을 의미하며, clockwise는 색을 지정할 때 시계방향 순서로 돌 것인지 지정한다.
줄기-잎 그림
> data <- read.csv("C:/BNG/education.csv", header=T)
> str(data)
'data.frame': 50 obs. of 9 variables:
$ state : chr "Alabama" "Alaska" "Arizona" "Arkansas" ...
$ reading : int 557 520 516 572 500 568 509 495 497 490 ...
$ math : int 552 516 521 572 513 575 513 498 498 491 ...
$ writing : int 549 492 497 556 498 555 512 484 480 479 ...
$ percent_graduates_sat: int 7 46 26 5 49 20 83 71 59 71 ...
$ pupil_staff_ratio : num 6.7 7.9 10.4 6.8 10.9 8.1 6.6 7.9 8.1 7 ...
$ dropout_rate : num 2.3 7.3 7.6 4.6 5.5 6.9 2.1 5.5 3.8 4.6 ...
$ Latitude : num 32.8 61.4 33.7 35 36.1 ...
$ Longitude : num -86.8 -152.4 -111.4 -92.4 -119.7 ...이번엔 50 X 9의 education 데이터를 불러왔다.
> stem(data$math)# data 파일 안에 있는 math 변수에 대해서 줄기-잎 그림 그리기
The decimal point is 1 digit(s) to the right of the |
46 | 7
48 | 16688
50 | 112225671233368
52 | 13561
54 | 02662488
56 | 581235
58 | 934
60 | 0034895stem()을 통하여 줄기-잎 그림을 볼 수 있다.
scale=2 옵션을 사용하면 줄기의 길이를 2배로 늘려서 좀 더 자세한 분포를 확인할 수 있다.
히스토그램
히스토그램은 연속형 변수에 대한 시각화 중에서 일반적으로 가장 선호하는 그래프이다.
R에 내장된 iris 데이터를 통하여 히스토그램을 그려보도록 하자.
hist(iris$Sepal.Length) # iris 파일 안에 있는 Sepal.Length 변수에 대한 히스토그램hist() 함수를 통해 그릴 수 있다.
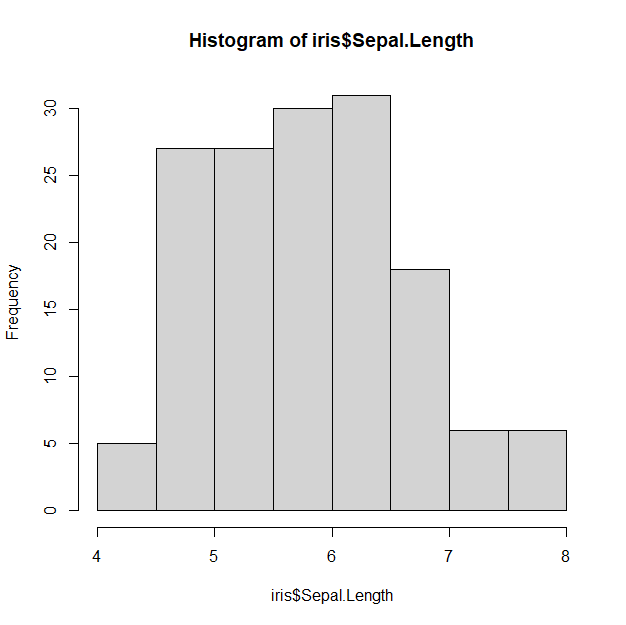
위가 Sepal.Length에 대한 히스토그램이다. 여기서는 Y축이 도수(빈도)로 나타났다.
hist(iris$Sepal.Length, breaks="Sturges", prob=T)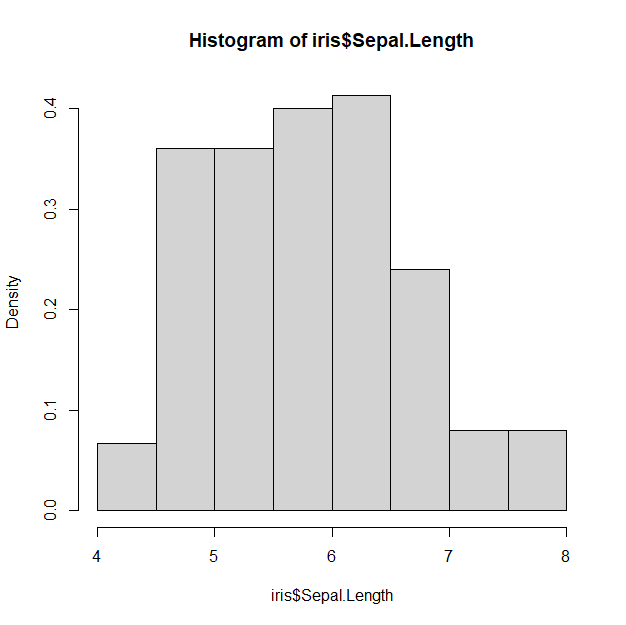
위의 히스토그램은 prob=T로 설정하여 막대높이를 상대도수로 표시하였다.
Sturges 옵션은 자료에 맞추어 구간의 수를 자동으로 계산한다는 의미이다.
도수로 표시한 히스토그램과 상대도수로 표시한 히스토그램 중 어떤 것이 나은가?
일반적으로는 상대도수로 많이 표현을 한다.
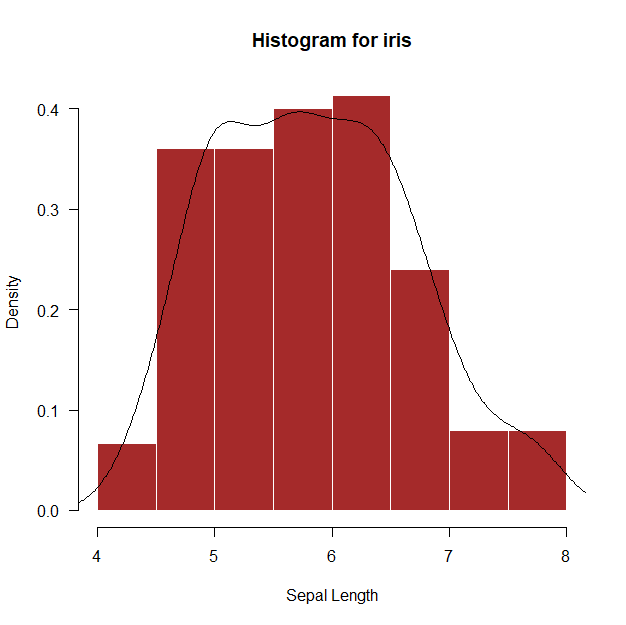
이 히스토그램을 통해서 알 수 있는 사실은 전체 데이터가 4~8 범위에서 존재하며,
4.5~6.5 사이에 가장 데이터가 많이 밀집되어 있는 것을 알 수 있다.
hist(iris$Sepal.Length,
main="Histogram for iris", xlab="Sepal Length", border="white", col="brown",
xlim=c(4,8), las=1, prob = TRUE)
lines(density(iris$Sepal.Length)) # line() : 선그래프 추가, density() : 밀도함수 그리기위처럼 여러가지 옵션을 추가할 수 있는데,
border는 막대 테두리선의 색깔이고 col은 막대 속의 색깔, las는 X축 데이터 글자를 배열하는 방식을 나타내는 것이고, xlim은 히스토그램을 그릴 때 x축의 범위를 조정할 수 있다.
lines(density())를 활용하면 히스토그램에 밀도함수 선 그래프를 추가할 수 있다.
hist(iris$Sepal.Length,
main="Histogram for iris", xlab="Sepal Length", border="white", col="brown",
xlim=c(4,8), las=1, breaks=2, prob = TRUE) # breaks = 2 : 계급구간을 2개로 설정
hist(iris$Sepal.Length,
main="Histogram for iris", xlab="Sepal Length", border="white", col="brown",
xlim=c(4,8), las=1, breaks=8, prob = TRUE) # breaks = 8 : 계급구간을 8개로 설정
hist(iris$Sepal.Length,
main="Histogram for iris", xlab="Sepal Length", border="white", col="brown",
xlim=c(4,8), las=1, breaks=15, prob = TRUE) # breaks = 15 : 계급구간을 15개로 설정
hist(iris$Sepal.Length,
main="Histogram for iris", xlab="Sepal Length", border="white", col="brown",
xlim=c(4,8), las=1, breaks=40, prob = TRUE) # 계급 구간 수 = 40위와 같이 계급 구간 수를 조정하여 히스토그램을 살펴보았다.
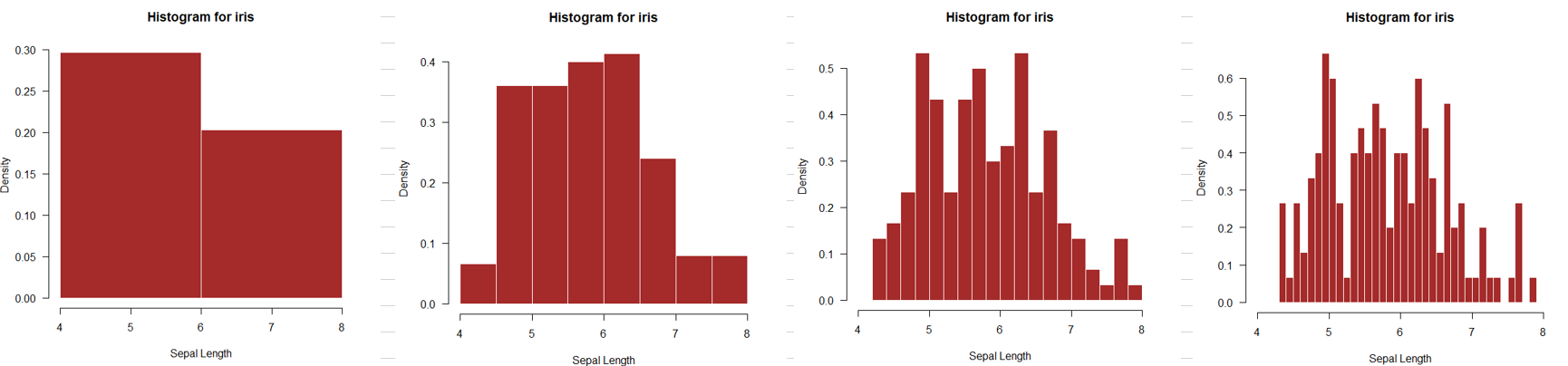
똑같은 변수에 대한 히스토그램이라도 계급구간의 개수가 증가할수록 히스토그램이 더 세밀해지는 면은 있지만, 전반적으로 분포의 형태를 파악하기에는 어려움이 있다.
계급 구간의 수가 너무 많으면 분포가 울퉁불퉁해서 해석하기 어렵기 때문에 알맞는 계급 구간의 수를 판단하여 시각화를 할 필요가 있다.
+ 계급 구간의 수를 12로 설정했을 때는 계급 구간을 8로 설정했을 때와 동일하게 나온다. why?
상자 그림
상자 그림은 연속형 변수에 대한 시각화 방법이다.
boxplot() 함수를 사용하여 그릴 수 있다.
boxplot(iris$Sepal.Width, main="Boxplot")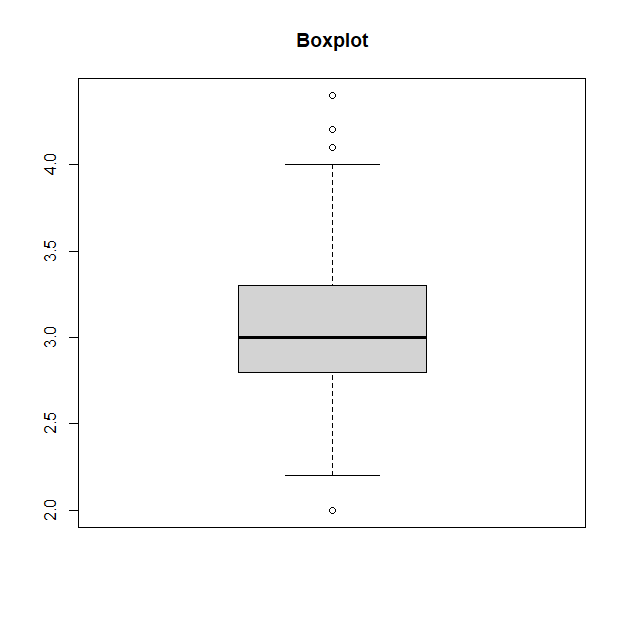
iris 데이터의 Sepal.Width 변수 데이터에 대한 box plot이다.
밀도 함수 그리기
연속형 변수에 대하여 밀도 함수를 그릴 수 있다.
plot(density())를 사용하며, rug()를 통하여 밀도에 대한 추가정보를 포함할 수 있다.
> geyser <- read.csv("C:/BNG/geyser.csv", header = T)
> str(geyser)
'data.frame': 299 obs. of 2 variables:
$ waiting : int 80 71 57 80 75 77 60 86 77 56 ...
$ duration: num 4.02 2.15 4 4 4 ...이번에는 299 X 2의 geyser 데이터를 통하여 밀도 함수를 그려보도록 하자.
plot(density(geyser$duration), main="Kernel Density Estimation", xlab="Duration")
rug(geyser$duration) # X-축에 데이터의 밀도를 표시. plot()함수와 rug() 함수는 항상 함께
# rug() : 데이터의 조밀한 정도(밀도)를 X축에 선으로 표시하는 함수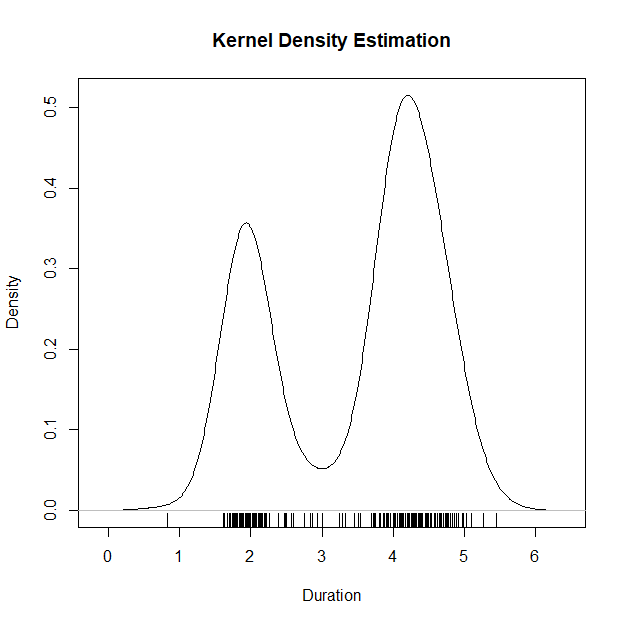
위와 같이 밀도 함수를 표현할 수 있다.
'복수전공' 카테고리의 다른 글
| [데이터 시각화] 4. 비교 시각화 (0) | 2021.10.25 |
|---|---|
| [데이터 시각화] 3. 시간 시각화 (0) | 2021.10.24 |
| [데이터 시각화] 1. 데이터 입출력 (0) | 2021.10.23 |
| [범주형 데이터분석] 1. 회귀 (0) | 2021.10.22 |
| [현대사회의 데이터와 통계학] 3. Numpy : 배열의 인덱싱과 슬라이싱 (0) | 2021.10.20 |
블로그의 정보
Hi Rev
Rev_