[데이터 시각화] 5. 모자이크 플롯
by Rev_모자이크 플롯은 범주형 변수들 간의 관련성을 시각화 한다.
mosaic 시각화는 교차점주에 대한 특징에 초점을 둔다. (예시) 성별이 남자이면서, 연령이 50대 이상, 학력이 대졸 이상인 사람은 신용도가 좋음
형태는 타일처럼 사각형의 크기에 따라서 범주형 변수의 빈도를 표현한다.
install.packages("vcd")
library(vcd)
UCBAdmissions <- read.csv("C:/BNG/UCBAdmissions.csv", header=T)
> str(UCBAdmissions)
'data.frame': 24 obs. of 5 variables:
$ X : int 1 2 3 4 5 6 7 8 9 10 ...
$ Admit : chr "Admitted" "Rejected" "Admitted" "Rejected" ...
$ Gender: chr "Male" "Male" "Female" "Female" ...
$ Dept : chr "A" "A" "A" "A" ...
$ Freq : int 512 313 89 19 353 207 17 8 120 205 ...
모자이크 플롯 분석을 위해 vcd 패키지를 설치하고, UCBAdmissions 라는 데이터를 불러왔다.
UCBAdmissions <- UCBAdmissions[, -1]여기서 첫 번째 변수인 X는 단지 일련번호에 불과하기 때문에 분석에 필요하지 않다.
그래서 첫번째 변수를 제거해 주었다. [, -1]의 의미는 첫번째 변수를 제거한다는 의미이다.
이제 모자이크 플롯 실습을 해보도록 하자.
mosaic( ~ Admit + Gender + Dept, data=UCBAdmissions)위의 ~ Admit + Gender + Dept에서 변수의 순서가 가장 중요하다.
여기서 ~은 무엇을 의미하는 걸까?
예시로 y ~ x1 + x2 라는 데이터가 있다고 가정할 때,
~의 왼쪽 y는 종속변수를 의미한다. 그리고 좌표평면에는 Y축을 의미한다.
~의 오른쪽 x1, x2는 독립변수를 의미한다. 그리고 좌표평면에서는 X축을 의미한다.
여기에서는 종속변수가 없기 때문에 Admit, Gender, Dept 변수들 간의 관련성만 분석한다.

출력된 그래프를 살펴보면, 제일 먼저 Admit 범주부터 나누고, 그 다음에 Gender 범주로 나누고, 맨 마지막에 Dept 범주로 나누게 된 결과를 볼 수 있다.
이 데이터를 간단하게 분석해보자면, 위쪽 빨강 박스는 입학허가(Admitted)가 난 A학과의 남학생을 의미하고, 아래쪽 빨강 박스는 불합격 된 F학과의 여학생 비율임을 알 수 있다.
위의 데이터를 좀 더 다채로운 그래프로 나타내보자.
mosaic( ~ Dept + Gender + Admit, data=UCBAdmissions,
highlighting="Admit", highlighting_fill=c("lightblue", "pink"),
direction=c("v","h","v"))여기서는 Dept, Gender, Admit의 순서로 나누었다.
highlighting="Admit"을 통하여 Admit 변수에 색 강조를 지정하였다. 강조하고 싶은 색상은 highlighting_fill을 통하여 연한 파란색과 분홍색으로 지정하였다.
direction은 범주형 변수를 나누는 방법인데, v는 수직으로 나누는 것이고 h는 수평으로 나누는 것이다. 여기서는 Dept 변수는 수직, Gender은 수평, Admit는 수직으로 각각 나누었다.

하늘색은 입학 승인, 분홍색은 입학 거절을 의미한다.
A학과의 결과를 살펴보면 합격자 수는 남자가 여자에 비해서 더 많음을 알 수 있다. 그러나 합격자 비율로 따지만 여자가 더 높다. B학과의 경우에는 남녀 합격자 비율이 비슷하다고 할 수 있다.
C학과의 결과를 살펴보면 합격자 수는 여학생이 더 많다. E학과에서도 여학생이 합격자 수가 더 많다.
A, B 학과는 여학생 지원자 수가 작다. 이 데이터에서 합격여부에 남녀차별은 존재하지 않았다고 판단할 수 있다. 지원자 수와 합격률을 함께 보고 판단할 필요가 있다.
mosaic( ~ Dept + Gender + Admit, data=UCBAdmissions,
highlighting="Admit", highlighting_fill=c("blue", "red"),
direction=c("v", "v", "h"))
mosaic( ~ Dept + Gender + Admit, data=UCBAdmissions,
highlighting="Admit", highlighting_fill=c("yellow", "green"),
direction=c("v", "h", "h"))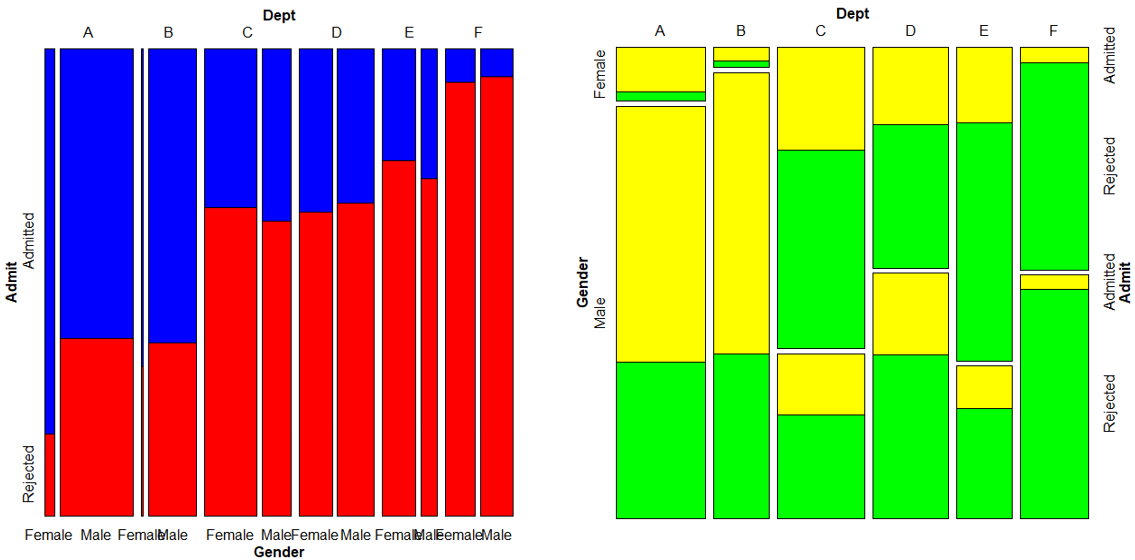
색상과 direction을 다르게 설정한다면 위와 같이 나타낼 수 있다.
그 다음으로는 실습을 위한 타이타닉 데이터를 불러왔다.
> Titanic <- read.csv("C:/BNG/Titanic.csv", header=T)
> str(Titanic)
'data.frame': 2201 obs. of 5 variables:
$ id : int 1 2 3 4 5 6 7 8 9 10 ...
$ Class : chr "3rd" "3rd" "3rd" "3rd" ...
$ Sex : chr "Male" "Male" "Male" "Male" ...
$ Age : chr "Child" "Child" "Child" "Child" ...
$ Survived: chr "No" "No" "No" "No" ...타이타닉 데이터는 2201 X 5 데이터이다. 객실, 성별, 성인여부, 생존여부에 대한 범주형 시각화를 하고자 한다.
mosaic( ~ Class + Sex + Age + Survived, data=Titanic,
highlighting="Survived", highlighting_fill=c("blue", "red"), # blue=no, red=yes
direction=c("v","h","v","h"))
여기에선 생존 여부에 색깔 강조를 지정하였다. 파란색이 사망이고 붉은색이 생존인 경우이다.
객실이 1등급인 경우, 생존자 수는 남자에 비해서 여자가 더 많다. 또한 (잘 보이진 않지만) 성인에 비해서 어린이의 생존율이 훨씬 더 높음을 알 수 있다.
객실이 2등급인 경우에는 1등급인 경우에 비해서 생존자 수와 생존률이 낮아졌지만, 여전히 남자에 비해 여자가 생존자 수와 생존률이 높다. 그리고 여기서도 성인에 비해서 어린이의 생존자 수와 생존률이 훨씬 높다.
객실이 3등급인 경우, 어린이 조차도 생존자 수가 많이 감소함을 알 수 있다.
결론적으로 객실의 등급이 높을 수록 여자와 어린아이의 생존율이 높다고 할 수 있다.
'복수전공' 카테고리의 다른 글
| [SAS 자료분석] 2. SAS 데이터 단계 (0) | 2021.10.31 |
|---|---|
| [범주형 데이터분석] 3. 주성분분석(PCA) (0) | 2021.10.30 |
| [SAS 자료분석] 1. SAS파일 다루기 (0) | 2021.10.25 |
| [범주형 데이터분석] 2. 선형대수학(Linear Algebra) (0) | 2021.10.25 |
| [데이터 시각화] 4. 비교 시각화 (0) | 2021.10.25 |
블로그의 정보
Hi Rev
Rev_