[범주형 데이터분석] 2. 선형대수학(Linear Algebra)
by Rev_데이터분석 알고리즘을 공부하기 위해서는 선형대수학을 필수적으로 알아야한다.
그러므로 이 수업에서는 선형대수의 기본적인 내용들도 담았다.
벡터의 내적
벡터란 1차원 배열을 말한다.
아래 x, y 두 벡터가 있다. 이 벡터들의 내적을 계산해보자.
x = np.array((0, -1, 3, -6)) # x = (0, -1, 3, -6)
y = np.array((1, 2, -3, 5)) # y = (1, 2, -3, 5)x.dot(y)y.dot(x)np.dot(x, y)x @ y벡터의 내적은 위와 같이 계산할 수 있다. 값은 모두 동일하게 -41이 나온다.
- 벡터의 길이와 내적

벡터 공간에서 벡터의 길이나 사이즈를 구할 때 norm(놈)을 사용하는데 위와 같이 구할 수 있다. 피타고라스의 정리와 같은 원리이다. 원점에서 점 x = (a, b)까지의 거리를 나타낸다.

두 벡터 x, y사이의 각을 𝜃라고 할 때 두 벡터의 내적은 위와 같다.
여기서 사잇각의 코사인값은 계산한다면,
x.dot(y) / np.sqrt(x.dot(x) * y.dot(y))로 나타낼 수 있을 것이다.
- 직교하는 벡터
직교 벡터는 두 벡터 사이의 각도가 90도를 이루는 것을 의미한다.
x = np.array((-1, 2))
y = np.array((2, 1))
np.sum(x * y)[Out] 0
두 벡터가 직교하면 사잇각의 코사인 값이 0이므로 내적도 0이다.
행렬 곱셈
두 행렬 A(m X n), B(n X p)의 곱셈은 A행벡터와 B열벡터들을 mp번 내적해서 m X p 행렬을 만드는 것이다. 여기서 n 값이 서로 동일해야만 연산을 할 수 있다는 점 유의하자.
- 전치 행렬
m X n 행렬을 전치시켜면 행과 열이 바뀌어 n X m 행렬이 된다.
A = np.array([0, 1, 2, 3]).reshape(2, 2)
B = np.array([3, 2, 0, 1]).reshape(2, 2)
A.T[Out] array([[0, 2],
[1, 3]])
일반적으로 A.T 코드를 사용하면 된다.
- 역행렬

n X n 행렬 A에 대해 위 식을 만족하는 역행렬을 의미한다.
Ainv = np.linalg.inv(A)
Ainv[Out] array([[-1.5, 0.5],
[ 1. , 0. ]])
역행렬을 구하는 함수는 위와 같이 사용할 수 있다.
- 행렬식
np.linalg.det(A)[Out] -2.0
행렬식은 위와 같은 함수로 구할 수 있다.

단순한 2 X 2 행렬의 행렬식을 보자면 위와 같은데, 이것을 보면 대각행렬의 행렬식은 대각선 원소들의 곱과 같다는 것을 알 수 있다.
또한 행렬식이 존재하여야만 역행렬을 구할 수 있는데, 그 이유는 행렬식의 값은 역행렬을 계산할 때 분모로 쓰이기 때문이다.
선형 독립, 선형 종속
va = np.array([-1, 0, 4]); vb = np.array([3, 0, -12]); vc = np.array([1, 0, 4]);
MA = np.array([va, vb, vc])
MA실행 결과 : array([[ -1, 0, 4],
[ 3, 0, -12],
[ 1, 0, 4]])
위에서 만든 행렬로 예시를 들어보자.
여기서 1행과 2행은 선형종속관계이다. 그 이유는 1행에 -3을 곱한 값이 2행이 되기 때문이다.
따라서 MA의 행렬식은 0이다. 행렬식이 0이므로 역행렬도 존재할 수 없다. 이런 행렬을 singular matrix(특이행렬)이라고 한다.
- 선형결합(linear combination)
길이가 같은 벡터들에 각각 상수를 곱해서 더하면 새로운 벡터가 생긴다. 이를 벡터들의 선형결합이라고 한다.
2차원 평면상에 두 벡터 v1 = (1, 0) v2 = (0, 1)이 있다고 가정하면 두 벡터에 각각 상수를 곱해서 더하면 그 공간상에 모든 점을 다 만들 수 있다.
하지만 두 벡터 v1 = (1, 0) v3 = (2, 0) 를 아무리 선형결합시키더라도 2차원 공간을 만들 수 없고, 1차원 직선만 만들 수 있다.
그 이유는 v1과 v2는 선형독립이지만, v1과 v3은 선형종속이기 때문이다.
고유값, 고유벡터
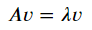
n X n 행렬에 A에 대해 위 식을 만족하는 벡터 u를 A의 고유벡터라 하고 스칼라값을 고유값이라고 한다.
PCV등 차원축소를 할 때 주로 고유벡터를 사용한다.
eig() 함수를 이용한다면 간단히 고유벡터와 고유값을 구할 수 있다.
'복수전공' 카테고리의 다른 글
| [데이터 시각화] 5. 모자이크 플롯 (0) | 2021.10.27 |
|---|---|
| [SAS 자료분석] 1. SAS파일 다루기 (0) | 2021.10.25 |
| [데이터 시각화] 4. 비교 시각화 (0) | 2021.10.25 |
| [데이터 시각화] 3. 시간 시각화 (0) | 2021.10.24 |
| [데이터 시각화] 2. 분포 시각화 (0) | 2021.10.23 |
블로그의 정보
Hi Rev
Rev_